Calculadora de Matrices
El método matricial para resolver sistemas de ecuaciones también se conoce como método Row Echelon. El método de matriz es similar al método de eliminación, pero es mucho más limpio que el método de eliminación. Todo esto gracias igual con la calculadora de matrices.
Resolver sistemas de ecuaciones mediante el método de matriz implica expresar el sistema de ecuaciones en forma de matriz y luego reducir esa matriz a lo que se conoce como forma de escalón de fila. (Todo esto puede ser resuelto con la ayuda de una calculadora de matrices).
Tabla de contenidos
Resolver ecuaciones con el método matricial con Calculadora de matrices
A continuación hay dos ejemplos de matrices en forma de escalón de fila
![]()

La primera es una matriz de 2 x 2 en forma Row Echelon y la segunda es una matriz de 3 x 3 en forma Row Echelon.
Expresando sistemas de ecuaciones como matrices (resolver con calculadora de matrices)
Dado el siguiente sistema de ecuaciones:
![]()
Los dos sistemas de ecuaciones variables anteriores se pueden expresar como un sistema matricial de la siguiente manera
![]()
Si resolvemos lo anterior usando las reglas de multiplicación de matrices, deberíamos terminar con el sistema de ecuaciones con el que comenzamos. Podemos modificar aún más las matrices anteriores y ocultar la matriz que contiene las variables. No lo eliminamos, solo lo ocultamos para que podamos hacer nuestros cálculos más limpios.
![]()
Lo anterior se modifica aún más en una matriz única como a continuación
![]()
Muchas veces se dibuja una línea vertical para indicar que la columna más a la derecha representa las entradas a la derecha del signo igual en el sistema de ecuaciones.
![]()
Lo mismo puede hacerse para un sistema de ecuaciones con tres variables.

Lo anterior se puede expresar como un producto de matrices en la forma:
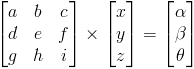
Ocultando la matriz que contiene las variables, podemos expresar lo anterior como:
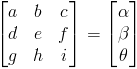
Luego poniéndolo todo en una matriz:
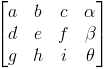
o como
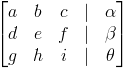
La forma anterior se conoce como matriz aumentada . En la matriz aumentada anterior, sabemos que las entradas a la izquierda representan los coeficientes de las variables en el sistema de ecuaciones.
Método de reducción a la forma escalonada de fila
Antes de leer esta sección, debe echar un vistazo a la sección de Reducción a Echelon en la sección Matrices.
Ahora que sabe cómo reducir una matriz a Row Echelon Form, veamos cómo aplicar el algoritmo a las matrices aumentadas formadas a partir de sistemas de ecuaciones.
Ejemplo 1:
Encuentre la solución para el siguiente sistema de ecuaciones
![]()
Solución:
El primer paso es expresar el sistema de ecuaciones anterior como una matriz aumentada.
![]()
A continuación etiquetamos las filas:
![]()
Ahora comenzamos a reducir la matriz a la forma escalonada de fila. Primero cambiamos el coeficiente principal de la primera fila a 1.
Logramos esto multiplicando R 1 por -1 ⁄ 3 :
![]()
A continuación, cambiamos el coeficiente en la segunda fila que se encuentra debajo del coeficiente principal en la primera fila. Esto se logra multiplicando R 2 por -1 ⁄ 5 y luego sumando el resultado a R 1 .
![]()
Añadiendo el resultado a R’ 1 :
![]()
Así que ahora nuestra nueva matriz se ve así:
![]()
En este punto, reintroducimos las variables en la fila 2 ya que ahora tendremos una ecuación de una variable:
![]()
Podemos resolver para y a partir de la ecuación anterior:
![]()
![]()
Ahora que tenemos y , podemos usar la sustitución inversa para resolver x sustituyendo y en las dos ecuaciones variables formadas a partir de R ‘ 1 :
![]()
![]()
![]()
Por lo tanto, la solución al sistema de ecuaciones es {x, y} = {2, -2}
Ejemplo 2:
Resolver para x, y y z en el sistema de ecuaciones a continuación
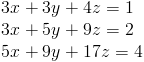
Solución:
El primer paso es convertir tres sistemas variables de ecuaciones en una matriz aumentada de 3×4.
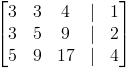
A continuación etiquetamos las filas de la matriz:
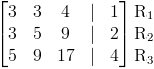
Dado que en la matriz aumentada anterior no podemos encontrar ninguna fila con uno como coeficiente principal, no necesitamos realizar una operación de cambio de fila. Sin embargo, necesitamos modificar la fila 1 de modo que su coeficiente principal sea 1.
Podemos lograr esto multiplicando la fila 1 por 1 ⁄ 3 :

A continuación, debemos cambiar todas las entradas por debajo del coeficiente principal de la primera fila a ceros.
Para la segunda fila, podemos lograr esto multiplicando primero por -1 ⁄ 3 y luego agregando el resultado a la fila 1.
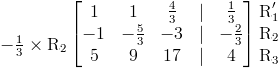
Agregando el resultado a la fila 1:

Luego pasamos a la fila 3; aquí multiplicamos la fila por -1 ⁄ 5 y luego agregamos el resultado a la fila 1 para poner a cero el primer elemento.
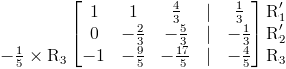
Agregando el resultado a la fila 1:
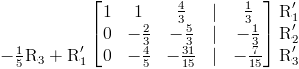
Necesitamos que el elemento principal en la segunda fila también sea uno. Obtenemos este resultado multiplicando la segunda fila por -3 ⁄ 2 :
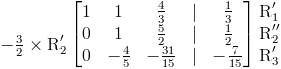
A continuación, ponemos a cero el elemento en la fila tres debajo del coeficiente principal en la fila dos. Para lograr esto, multiplicamos la tercera fila por 5 ⁄ 4

Agregando el resultado a la fila 2:
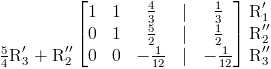
Finalmente multiplicamos la fila 3 por -12 para tener el elemento principal de la tercera fila como uno:
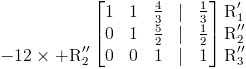
De la matriz anterior, resolvemos las variables que comienzan con z en la última fila
![]()
A continuación, resolvemos y sustituyendo z en la ecuación formada por la segunda fila:
![]()
![]()
![]()
Finalmente, resolvemos x sustituyendo los valores de y y z en la ecuación formada por la primera fila:
![]()
![]()
![]()
Por lo tanto, la solución al sistema de ecuaciones es {x, y, z} = {1, -2,1}
