Calculadora integrales

Una calculadora de integrales te ayudará a realizar cálculos matemáticos avanzados relacionados a, evidentemente, las integrales. Sus versiones más eficientes soportan tanto integrales indefinidas como definidas, incluyendo, por supuesto, funciones de integración con diversas variables.

¿Te gustaría conocer más sobre ellas? De ser así ¡Te invitamos a continuar leyendo! En este artículo te proporcionaremos toda la información que necesitas para comprenderlas.

¿Cómo surgió la calculadora de integrales?

Se dice que los científicos, investigaban el cómo calcular las áreas de las superficies, volúmenes de cuerpo sólidos y figuras planas. Fue entonces cuando se inclinaron a los problemas de hidrodinámica, estadística entre otros dominios físicos.

Para entender mejor dicho tema, señalaremos un ejemplo el cual se vinculó al desarrollo del cálculo integral; fue el haber encontrado la ley del movimiento del objeto, a lo largo de una línea, conociendo la velocidad del objeto.

En consecuencia, el cálculo integral evoluciona como un dominio de análisis matemático, el cual se incrementa como resultado, la solución de dos problemas claves: el primero se basa en adquirir la función, estableciendo el área limitada por un gráfico en particular o la superficie tridimensional de ciertos intervalos.

En definitiva, el primer problema, incitó el desarrollo del significado analítico de una integral y el segundo problema, le da paso al surgimiento del concepto de integral definida. Ahora bien, las integrales se emplean en diversos dominios de computación e investigación.

Por otro lado, tenemos que el cálculo integral se utiliza, para dar con el resultado del valor promedio de una función, en un intervalo dado, y de esta manera hacer los cálculos de las áreas entre curvas, estableciendo los volúmenes de objetos, de las regiones giratorias u otras.

Aparte, el cálculo integral es aplicado de manera amplia en física: se emplea para calcular la cantidad de un determinado trabajo para rotar un objeto, solucionar problemas de cinemática, investigar la interacción y movimiento de objetos, de esta manera dar con el centro de masa, evaluando la posibilidad de algunos eventos. Por tal motivo la comprensión del cálculo integral, viene siendo de gran importancia en diversos dominios.

¿Cuáles son las variantes que procesa la calculadora de integrales?

Existen dos tipos de integrales. Las indefinidas y las definidas. Una integral indefinida denota una función que conlleva a una derivada, produciendo una función dada, resaltando que las integrales indefinidas no poseen un límite de integración.

Integración indefinida

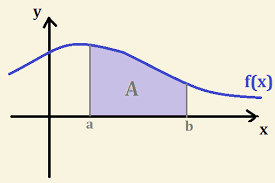
Para ser más explícitos, la integración indefinida, viene siendo la operación opuesta a la diferencia analítica. Por lo tanto, la ecuación para una integral indefinida se describe de la siguiente manera: en cuanto a su forma básica, y en el contexto de una doble función, la integral definida viene siendo igual al área, bajo la curva de la función dentro de un intervalo dado.

En consecuencia, uno de los fundadores del cálculo integral llamado Riemann, explica que la integral definida, se considera el resultado de un procedimiento limitante, el cual une un área entre dos curvas, al ser divididas el área en dos verticales delgadas.

Integración definida

Por lo que la ecuación de una integral definida, se emplea de la siguiente manera: la integral definida de A a B con respecto A. No obstante, podemos encontrar diversas clases de integrales definidas, las cuales se distinguen, de acuerdo al límite de la suma integral tal como: integrales impropias y propias y por otra parte por el número de las variables en la función bien sean: triples, múltiples e integrales dobles.

Los anti-derivados

Cuando hablamos de anti-derivados, nos referimos a una parte fundamental de la integración, puesto que la anti-derivada de una función regresa a la función original. Es decir, si el cálculo anti-derivado de f determina la derivada del cálculo de una función anti-derivada teniendo como resultado una función anti-derivada para.

Hacemos la demostración mediante un ejemplo explícito: la derivada de igual ‘A’, viene siendo una derivada para. Entonces la definición precisa de una anti-derivada queda de la siguiente manera: la función es una anti-derivada de la función en el intervalo si es para todos, ya que la definición de anti-derivada se emplea para el cálculo de distintos tipos de integrales.

Es muy significativo tener en cuenta, que la derivada de una constante es igual a 0, o simplemente la anti-derivada simboliza una familia de anti-derivados que se diferencia de una constante C.

¿Qué tipo de calculadora de integrales puedo encontrar ONLINE?

A través de internet encontrarás una amplia variedad de calculadora de integrales. Sin embargo, no todas obedecerán las mismas condiciones, ni mucho menos, la forma de derivar los procesos. Hay algunas que podrán soportar llevar a cabo ciertos cálculos, mientras que otras no.

Hay distintos medios a través de los cuales puedes llevar a cabo la búsqueda de una calculadora de integrales. Google, por evidencia, es la principal fuente. Te conducirá a un listado de páginas que te proporcionarán, algunas de ellas, una versión muy completa que te permitirá calcular las integrales y sus amplias variantes.

Sin embargo, también puedes encontrar algunas en versión de aplicaciones a través de tiendas oficiales –como Google Play o Play Store-, como, de igual manera, hay algunas otras que podrás encontrar en tiendas no oficiales. Generalmente vienen en versiones (.APK), listas para ser instalada.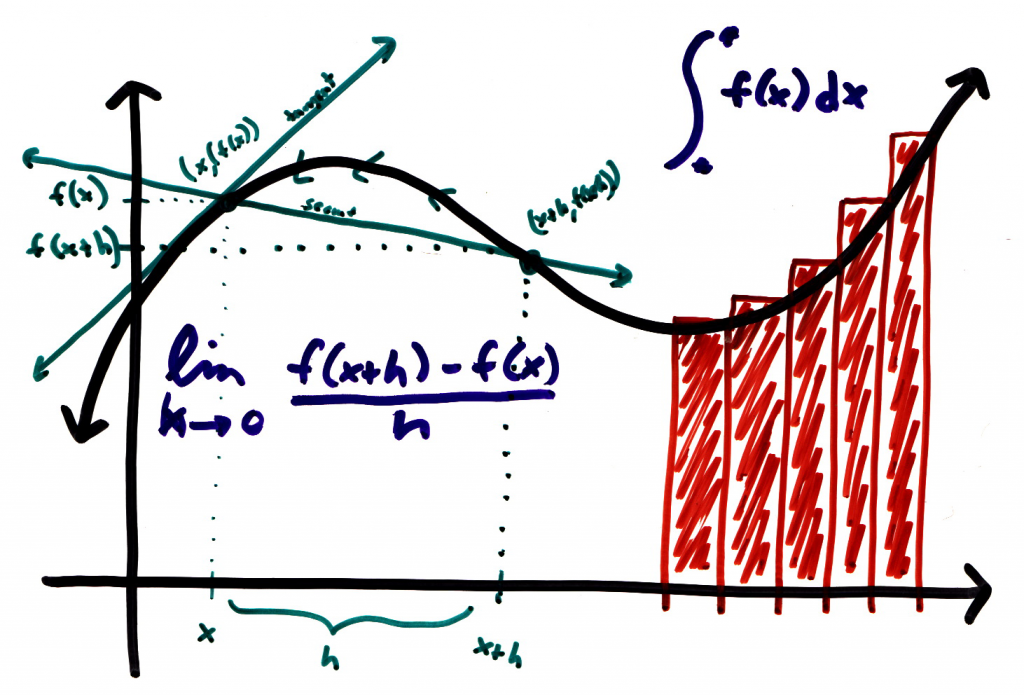

No se recomienda optar por aquellas tiendas o desarrolladores que no tienen referencias positivas. De hecho, de tener queja, es mejor obviarlas. Muchas de ellas son usadas con el objetivo de brindar aplicaciones con virus informáticos que terminarán dañando a nuestro dispositivo.

Siempre se prevé optar por esta alternativa como última opción, si puede ser evitada, muchísimo mejor, en especial si se carece de experiencia en descargar a través de estos medios. Por norma general, mientras puedas decidir por las opciones oficiales, o, en caso de no poder hacerlo, no descargar ningún archivo, sino ir directamente a las páginas webs y realizar las operaciones desde ellas, será aún más favorable.

Lo ideal es disfrutar de un óptimo servicio –en este caso, de cálculo- y evitar inconvenientes a largo plazo. Esto solo puede lograrse actuando conscientemente, y decidiendo de la mejor manera.